Will the Plane Take-Off - Merged with MythBusters Show Thread
#161
So, do you like...stuff?
Join Date: May 2002
Location: PA/NJ, now in CA (SoCal), USA
Age: 44
Posts: 924
Likes: 0
Received 3 Likes
on
2 Posts
Originally Posted by fdl
Yes, mathematically you would think it infinitely gets closer to zero, but our eyes and experince tells us that when we throw a ball against the wall it DOES hit the wall and bounces back. So therefore that would imply that there was a limit to how many times the distance could be cut in half. Pick up a ball and prove it to yourself

I still dont know how many times it wouldbe cut in half. Its probably an integration problem with the limits going from 0 to (the distance from ball to wall minus the radius of the ball)
#162
Go Giants
If a snake is crawling in a plane at 1 MPH (from back to front) and the plane is going 100 MPH, is the snake going 101 mph?
#163
Senior Moderator
I honestly dont think time is a factor. But lets suppose that is it - then assume that the ball is travelling at 5mph and calculate the number of time the distance is cut in half

#164
Senior Moderator
Originally Posted by Whiskers
If a snake is crawling in a plane at 1 MPH (from back to front) and the plane is going 100 MPH, is the snake going 101 mph?
relative to the earth, yes.
#165
On the way!
Join Date: Oct 2001
Location: Orlando, FL
Age: 55
Posts: 3,715
Likes: 0
Received 0 Likes
on
0 Posts
Originally Posted by RogerPodacter
I think the trick with this problem is that this is also a funtion of TIME. Of course you can cut a distance in half an infinite number of times when time is not dependent. But a ball moving in a real world situation is also dependent on time, meaning the ball will eventually hit the wall.
I still dont know how many times it wouldbe cut in half. Its probably an integration problem with the limits going from 0 to (the distance from ball to wall minus the radius of the ball)
I still dont know how many times it wouldbe cut in half. Its probably an integration problem with the limits going from 0 to (the distance from ball to wall minus the radius of the ball)
If the ball took 3 seconds to hit the wall - it's still an infinite amount of times you could cut 3 seconds in half.
#168
Go Giants
Originally Posted by fdl
You and your friend are on a plane travelling 500mph. He is sitting 3 feet from you. You throw him a ball. How far did the ball travel?
#169
On the way!
Join Date: Oct 2001
Location: Orlando, FL
Age: 55
Posts: 3,715
Likes: 0
Received 0 Likes
on
0 Posts
Originally Posted by fdl
You and your friend are on a plane travelling 500mph. He is sitting 3 feet from you. You throw him a ball. How far did the ball travel?
#170
So, do you like...stuff?
Join Date: May 2002
Location: PA/NJ, now in CA (SoCal), USA
Age: 44
Posts: 924
Likes: 0
Received 3 Likes
on
2 Posts
Originally Posted by fdl
You and your friend are on a plane travelling 500mph. He is sitting 3 feet from you. You throw him a ball. How far did the ball travel?
I dont know the answer, but i know that the trajectory of the ball would be the diagonal of a right triangle. Knowing the forward speed of the plane, i think you would have to know how fast the ball was thrown to the friend as well.
#171
Three Wheelin'
Originally Posted by fdl
Is infinity a real, fixed number? Does it exist? And if so, what is it?
A boy is 10 feet from a wall, and throws a ball against the wall. As the ball travels towards the wall, the distance between the ball and the wall is cut in half (the ball is 5 feet from the wall), then that distance is cut in half again (now the ball is 2 1/2 feet from the wall), and so on and so on.....
How many times is the distance cut in half before the ball reaches the wall? EVen when the ball is as close as a fraction of a inch from the wall, that distance must still be cut in half before the ball can reach the wall. And as we know, the ball does eventually hit the wall. So how many times was the distance cut in half?
A boy is 10 feet from a wall, and throws a ball against the wall. As the ball travels towards the wall, the distance between the ball and the wall is cut in half (the ball is 5 feet from the wall), then that distance is cut in half again (now the ball is 2 1/2 feet from the wall), and so on and so on.....
How many times is the distance cut in half before the ball reaches the wall? EVen when the ball is as close as a fraction of a inch from the wall, that distance must still be cut in half before the ball can reach the wall. And as we know, the ball does eventually hit the wall. So how many times was the distance cut in half?
My logic is undeniable, my loigc si undneiable, ym oiglc si ebldneiuna...
My brain just melted.
#172
Senior Moderator
Originally Posted by RogerPodacter
pythagorean theorem?
I dont know the answer, but i know that the trajectory of the ball would be the diagonal of a right triangle. Knowing the forward speed of the plane, i think you would have to know how fast the ball was thrown to the friend as well.
I dont know the answer, but i know that the trajectory of the ball would be the diagonal of a right triangle. Knowing the forward speed of the plane, i think you would have to know how fast the ball was thrown to the friend as well.
ya probably. I guess that ones easy. Now back to my infinity question ....
#173
Senior Moderator
Originally Posted by levon1830
Okay, who even says that you have to divide the distance between the wall and the ball after the ball is thrown? Use subtraction!
My logic is undeniable, my loigc si undneiable, ym oiglc si ebldneiuna...
My brain just melted.
My logic is undeniable, my loigc si undneiable, ym oiglc si ebldneiuna...
My brain just melted.

It all becomes clearer on crystal meth.
#175
So, do you like...stuff?
Join Date: May 2002
Location: PA/NJ, now in CA (SoCal), USA
Age: 44
Posts: 924
Likes: 0
Received 3 Likes
on
2 Posts
Originally Posted by levon1830
Okay, who even says that you have to divide the distance between the wall and the ball after the ball is thrown? Use subtraction!
My logic is undeniable, my loigc si undneiable, ym oiglc si ebldneiuna...
My brain just melted.
My logic is undeniable, my loigc si undneiable, ym oiglc si ebldneiuna...
My brain just melted.

#176
Okay. The problem is that the question does not match the situation. Yes, you can keep cutting numbers in half inifnitely (unless you define something like a decimal followed by nine zeroes equals zero despite the existance of a tenth number). The ball will absolutely hit the wall but in order to figure that out you would not cut the distance in half over and over again, you would use a speed and time physics type of equation; therefore, the equation of cutting in half does not apply to the ball being thrown at the wall. Did that make any sense?
#177
Originally Posted by fdl
You and your friend are on a plane travelling 500mph. He is sitting 3 feet from you. You throw him a ball. How far did the ball travel?
#178
Senior Moderator
Originally Posted by RLToni
Okay. The problem is that the question does not match the situation. Yes, you can keep cutting numbers in half inifnitely (unless you define something like a decimal followed by nine zeroes equals zero despite the existance of a tenth number). The ball will absolutely hit the wall but in order to figure that out you would not cut the distance in half over and over again, you would use a speed and time physics type of equation; therefore, the equation of cutting in half does not apply to the ball being thrown at the wall. Did that make any sense?
Even when there is .000001 inches left to travel, the distance will at some point become .0000005 before it hits the wall. Mathematically we know that this function leads to infinity. But in the given scenario this number does somehow eventually reach 0. But how? Does it not imply that infinity in this context is a real tangible limit that gets reached at some point? If so, what is it?
#179
Where is my super sauce?
Originally Posted by fdl
Is infinity a real, fixed number? Does it exist? And if so, what is it?
A boy is 10 feet from a wall, and throws a ball against the wall. As the ball travels towards the wall, the distance between the ball and the wall is cut in half (the ball is 5 feet from the wall), then that distance is cut in half again (now the ball is 2 1/2 feet from the wall), and so on and so on.....
How many times is the distance cut in half before the ball reaches the wall? EVen when the ball is as close as a fraction of a inch from the wall, that distance must still be cut in half before the ball can reach the wall. And as we know, the ball does eventually hit the wall. So how many times was the distance cut in half?
A boy is 10 feet from a wall, and throws a ball against the wall. As the ball travels towards the wall, the distance between the ball and the wall is cut in half (the ball is 5 feet from the wall), then that distance is cut in half again (now the ball is 2 1/2 feet from the wall), and so on and so on.....
How many times is the distance cut in half before the ball reaches the wall? EVen when the ball is as close as a fraction of a inch from the wall, that distance must still be cut in half before the ball can reach the wall. And as we know, the ball does eventually hit the wall. So how many times was the distance cut in half?
#183
Team Owner
iTrader: (1)
Join Date: Sep 2002
Location: Fontana, California
Age: 47
Posts: 30,991
Received 582 Likes
on
346 Posts
Originally Posted by SwervinCL
Read the last 5 pages. The wheels have nothing to do with forward movement on a plane. The thrust produced from the engines will make the plane move forward reguardless of the speed the ground is moving at.
However, the conveyor belt matching the amount of movement the plane is attaining due to the thrust output COUNTERACTS ANY possibility of the plane moving forward. If the plane ISN'T moving, which it isn't, no air is moving over the wing, which DOESN'T produce Lift.
Thrust doesn't force air over the wing. Thrust only moves the plane to produce the movement of air over the wing to generate lift.
If the plane is stationary, no movement, no change in pressure over the wing, no lift, no takeoff.
#184
Yeehaw
Originally Posted by Sly Raskal
You're right the wheels have no bearing on this discussion because it's all about thrust and lift. The thrust moves the plane FORWARD. This forward movement causes the air to move over the wing. This air movement is what produces lift.
However, the conveyor belt matching the amount of movement the plane is attaining due to the thrust output COUNTERACTS ANY possibility of the plane moving forward. If the plane ISN'T moving, which it isn't, no air is moving over the wing, which DOESN'T produce Lift.
However, the conveyor belt matching the amount of movement the plane is attaining due to the thrust output COUNTERACTS ANY possibility of the plane moving forward. If the plane ISN'T moving, which it isn't, no air is moving over the wing, which DOESN'T produce Lift.
No it doesn't. The wheels spin faster, the plane moves forward just like it would normally.
Imagine there is zero friction in the wheels. The conveyor belt goes 100mph, so the wheels spin 100mph. The plane doesn't move (0 friction). Now, the plane turns on the jets, it starts moving forward.
All the wheels do is provide a way to keep the plane off the ground with minimum friction. They don't propel the plane. Your answer is wrong and there are numerous examples and links in the thread proving this...
#185
Senior Moderator
OK here is the answer:
It's a tough question, because the word "infinity" can mean different things in different contexts.
In mathematics, whether or not a certain concept exists can depend on the context in which you ask the question. If you want to know more about this, you can refer to a fuller explanation of how a mathematical concept can exist in some contexts but not in others.
Here are some of the contexts in which the question "is there such a thing as infinity" can be asked, and the answers appropriate for each context. The details are given afterwards.
1. In the context of a number system,
in which "infinity" would mean something one can treat like a number.
In this context, infinity does not exist.
2. In the context of a topological space,
in which "infinity" would mean something that certain sequences of numbers converge to.
In this context, infinity does exist.
3. In the context of measuring sizes of sets,
in which "infinity" means a measurement of the size of an infinite set.
In this context, such "infinity" concepts do exist but there are more than one of them, since not all infinite sets have the same size. So there does not exist any one single "infinity" concept; instead, there exists a whole collection of things called "infinite cardinal numbers".
--
In the context of a topological space.
You've probably never heard the term "topological space" before; it occurs in an advanced branch of mathematics. Don't worry; we don't need to get into that advanced area. All we need is the following rough idea:
Roughly speaking, a topological space is any collection of objects for which there is a definition of which sequences of objects converge to other objects, and which sequences don't.
The real number system is a topological space: there's a definition of what it means for a sequence of numbers to converge. For instance, the sequence 1.1, 1.01, 1.001, 1.0001, etc. converges to the number 1, while the sequence 1, 2, 1, 2, 1, 2, 1, 2, etc. does not converge to anything.
In areas such as calculus, one often speaks of a sequence like 1, 2, 3, 4, . . . as "converging to infinity". Is this just a convenient phrase, or can there actually exist an object "infinity" that this sequence is converging to?
In other words, the question is: does there exist some topological space (that is, a set of objects plus a definition of what convergence means) which, as well as including the familiar real numbers we are used to, also includes an "infinity" concept to which some sequences of real numbers converge?
The answer is yes.
It is important to realize, though, that this topological space is not a number system. Although it includes an additional object called "infinity" as well as the familiar real numbers, you cannot add, subtract, multiply, or divide this additional object the way you can numbers.
Sometimes you will see a statement like "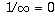 ". This does not really mean what it seems to say. You are not really dividing 1 by infinity. Instead, it is a statement about sequences. What it means is that if a sequence
". This does not really mean what it seems to say. You are not really dividing 1 by infinity. Instead, it is a statement about sequences. What it means is that if a sequence  ,
,  ,
,  . . . converges to infinity, then the sequence of reciprocals
. . . converges to infinity, then the sequence of reciprocals 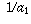 ,
, 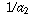 ,
, 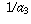 , . . . converges to zero.
, . . . converges to zero.
(Similar looking expressions like "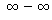 " don't make any sense, for just because two sequences
" don't make any sense, for just because two sequences 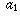 ,
, 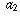 ,
, 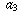 , . . . and
, . . . and 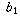 ,
, 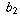 ,
, 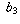 , . . . each converge to infinity tells you nothing about what the sequence
, . . . each converge to infinity tells you nothing about what the sequence 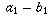 ,
, 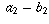 ,
, 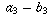 , . . . does.)
, . . . does.)
More Information on Why "Infinity" Does Exist in the Context of A Topological Space
It's a tough question, because the word "infinity" can mean different things in different contexts.
In mathematics, whether or not a certain concept exists can depend on the context in which you ask the question. If you want to know more about this, you can refer to a fuller explanation of how a mathematical concept can exist in some contexts but not in others.
Here are some of the contexts in which the question "is there such a thing as infinity" can be asked, and the answers appropriate for each context. The details are given afterwards.
1. In the context of a number system,
in which "infinity" would mean something one can treat like a number.
In this context, infinity does not exist.
2. In the context of a topological space,
in which "infinity" would mean something that certain sequences of numbers converge to.
In this context, infinity does exist.
3. In the context of measuring sizes of sets,
in which "infinity" means a measurement of the size of an infinite set.
In this context, such "infinity" concepts do exist but there are more than one of them, since not all infinite sets have the same size. So there does not exist any one single "infinity" concept; instead, there exists a whole collection of things called "infinite cardinal numbers".
--
In the context of a topological space.
You've probably never heard the term "topological space" before; it occurs in an advanced branch of mathematics. Don't worry; we don't need to get into that advanced area. All we need is the following rough idea:
Roughly speaking, a topological space is any collection of objects for which there is a definition of which sequences of objects converge to other objects, and which sequences don't.
The real number system is a topological space: there's a definition of what it means for a sequence of numbers to converge. For instance, the sequence 1.1, 1.01, 1.001, 1.0001, etc. converges to the number 1, while the sequence 1, 2, 1, 2, 1, 2, 1, 2, etc. does not converge to anything.
In areas such as calculus, one often speaks of a sequence like 1, 2, 3, 4, . . . as "converging to infinity". Is this just a convenient phrase, or can there actually exist an object "infinity" that this sequence is converging to?
In other words, the question is: does there exist some topological space (that is, a set of objects plus a definition of what convergence means) which, as well as including the familiar real numbers we are used to, also includes an "infinity" concept to which some sequences of real numbers converge?
The answer is yes.
It is important to realize, though, that this topological space is not a number system. Although it includes an additional object called "infinity" as well as the familiar real numbers, you cannot add, subtract, multiply, or divide this additional object the way you can numbers.
Sometimes you will see a statement like "
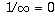 ". This does not really mean what it seems to say. You are not really dividing 1 by infinity. Instead, it is a statement about sequences. What it means is that if a sequence
". This does not really mean what it seems to say. You are not really dividing 1 by infinity. Instead, it is a statement about sequences. What it means is that if a sequence 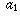 ,
, 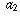 ,
, 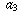 . . . converges to infinity, then the sequence of reciprocals
. . . converges to infinity, then the sequence of reciprocals 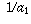 ,
, 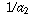 ,
, 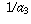 , . . . converges to zero.
, . . . converges to zero.(Similar looking expressions like "
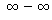 " don't make any sense, for just because two sequences
" don't make any sense, for just because two sequences 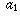 ,
, 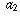 ,
, 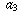 , . . . and
, . . . and 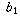 ,
, 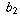 ,
, 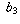 , . . . each converge to infinity tells you nothing about what the sequence
, . . . each converge to infinity tells you nothing about what the sequence 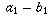 ,
, 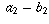 ,
, 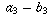 , . . . does.)
, . . . does.)More Information on Why "Infinity" Does Exist in the Context of A Topological Space
#186
Team Owner
iTrader: (1)
Join Date: Sep 2002
Location: Fontana, California
Age: 47
Posts: 30,991
Received 582 Likes
on
346 Posts
Originally Posted by BEETROOT
No it doesn't. The wheels spin faster, the plane moves forward just like it would normally.
Imagine there is zero friction in the wheels. The conveyor belt goes 100mph, so the wheels spin 100mph. The plane doesn't move (0 friction). Now, the plane turns on the jets, it starts moving forward.
All the wheels do is provide a way to keep the plane off the ground with minimum friction. They don't propel the plane. Your answer is wrong and there are numerous examples and links in the thread proving this...
Imagine there is zero friction in the wheels. The conveyor belt goes 100mph, so the wheels spin 100mph. The plane doesn't move (0 friction). Now, the plane turns on the jets, it starts moving forward.
All the wheels do is provide a way to keep the plane off the ground with minimum friction. They don't propel the plane. Your answer is wrong and there are numerous examples and links in the thread proving this...
#187
Yeehaw
Originally Posted by Sly Raskal
I should go out, buy a nice radio controlled plane, put it on a treadmill and fire the two of them up to show that the plane won't fly.
go nuts, it will fly just fine.
as has been mentioned numerous times, the thrust from a jet/propeller is entirely seperate from the wheels spinning. They can spin 20,000 rpm, the plane can still easily move forward.
http://www.straightdope.com/columns/060203.html
#188
So, do you like...stuff?
Join Date: May 2002
Location: PA/NJ, now in CA (SoCal), USA
Age: 44
Posts: 924
Likes: 0
Received 3 Likes
on
2 Posts
if you read the links in this thread, you will see that someone did indeed do that, bought a small plane, put it on a treadmill going maximum speed in opposite direction, and it did actually fly.
#189
Team Owner
iTrader: (1)
Join Date: Sep 2002
Location: Fontana, California
Age: 47
Posts: 30,991
Received 582 Likes
on
346 Posts
Originally Posted by RogerPodacter
if you read the links in this thread, you will see that someone did indeed do that, bought a small plane, put it on a treadmill going maximum speed in opposite direction, and it did actually fly.
But did they match the treadmill speed to the amount of thrust the plane produced and if so did it then fly?
#190
On the way!
Join Date: Oct 2001
Location: Orlando, FL
Age: 55
Posts: 3,715
Likes: 0
Received 0 Likes
on
0 Posts
Originally Posted by fdl
OK here is the answer:
It's a tough question, because the word "infinity" can mean different things in different contexts.
In mathematics, whether or not a certain concept exists can depend on the context in which you ask the question. If you want to know more about this, you can refer to a fuller explanation of how a mathematical concept can exist in some contexts but not in others.
Here are some of the contexts in which the question "is there such a thing as infinity" can be asked, and the answers appropriate for each context. The details are given afterwards.
1. In the context of a number system,
in which "infinity" would mean something one can treat like a number.
In this context, infinity does not exist.
2. In the context of a topological space,
in which "infinity" would mean something that certain sequences of numbers converge to.
In this context, infinity does exist.
3. In the context of measuring sizes of sets,
in which "infinity" means a measurement of the size of an infinite set.
In this context, such "infinity" concepts do exist but there are more than one of them, since not all infinite sets have the same size. So there does not exist any one single "infinity" concept; instead, there exists a whole collection of things called "infinite cardinal numbers".
--
In the context of a topological space.
You've probably never heard the term "topological space" before; it occurs in an advanced branch of mathematics. Don't worry; we don't need to get into that advanced area. All we need is the following rough idea:
Roughly speaking, a topological space is any collection of objects for which there is a definition of which sequences of objects converge to other objects, and which sequences don't.
The real number system is a topological space: there's a definition of what it means for a sequence of numbers to converge. For instance, the sequence 1.1, 1.01, 1.001, 1.0001, etc. converges to the number 1, while the sequence 1, 2, 1, 2, 1, 2, 1, 2, etc. does not converge to anything.
In areas such as calculus, one often speaks of a sequence like 1, 2, 3, 4, . . . as "converging to infinity". Is this just a convenient phrase, or can there actually exist an object "infinity" that this sequence is converging to?
In other words, the question is: does there exist some topological space (that is, a set of objects plus a definition of what convergence means) which, as well as including the familiar real numbers we are used to, also includes an "infinity" concept to which some sequences of real numbers converge?
The answer is yes.
It is important to realize, though, that this topological space is not a number system. Although it includes an additional object called "infinity" as well as the familiar real numbers, you cannot add, subtract, multiply, or divide this additional object the way you can numbers.
Sometimes you will see a statement like "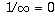 ". This does not really mean what it seems to say. You are not really dividing 1 by infinity. Instead, it is a statement about sequences. What it means is that if a sequence
". This does not really mean what it seems to say. You are not really dividing 1 by infinity. Instead, it is a statement about sequences. What it means is that if a sequence 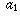 ,
, 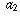 ,
, 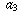 . . . converges to infinity, then the sequence of reciprocals
. . . converges to infinity, then the sequence of reciprocals 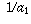 ,
, 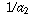 ,
, 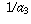 , . . . converges to zero.
, . . . converges to zero.
(Similar looking expressions like "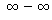 " don't make any sense, for just because two sequences
" don't make any sense, for just because two sequences 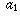 ,
, 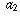 ,
, 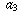 , . . . and
, . . . and 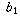 ,
, 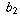 ,
, 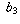 , . . . each converge to infinity tells you nothing about what the sequence
, . . . each converge to infinity tells you nothing about what the sequence 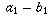 ,
, 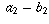 ,
, 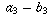 , . . . does.)
, . . . does.)
More Information on Why "Infinity" Does Exist in the Context of A Topological Space
It's a tough question, because the word "infinity" can mean different things in different contexts.
In mathematics, whether or not a certain concept exists can depend on the context in which you ask the question. If you want to know more about this, you can refer to a fuller explanation of how a mathematical concept can exist in some contexts but not in others.
Here are some of the contexts in which the question "is there such a thing as infinity" can be asked, and the answers appropriate for each context. The details are given afterwards.
1. In the context of a number system,
in which "infinity" would mean something one can treat like a number.
In this context, infinity does not exist.
2. In the context of a topological space,
in which "infinity" would mean something that certain sequences of numbers converge to.
In this context, infinity does exist.
3. In the context of measuring sizes of sets,
in which "infinity" means a measurement of the size of an infinite set.
In this context, such "infinity" concepts do exist but there are more than one of them, since not all infinite sets have the same size. So there does not exist any one single "infinity" concept; instead, there exists a whole collection of things called "infinite cardinal numbers".
--
In the context of a topological space.
You've probably never heard the term "topological space" before; it occurs in an advanced branch of mathematics. Don't worry; we don't need to get into that advanced area. All we need is the following rough idea:
Roughly speaking, a topological space is any collection of objects for which there is a definition of which sequences of objects converge to other objects, and which sequences don't.
The real number system is a topological space: there's a definition of what it means for a sequence of numbers to converge. For instance, the sequence 1.1, 1.01, 1.001, 1.0001, etc. converges to the number 1, while the sequence 1, 2, 1, 2, 1, 2, 1, 2, etc. does not converge to anything.
In areas such as calculus, one often speaks of a sequence like 1, 2, 3, 4, . . . as "converging to infinity". Is this just a convenient phrase, or can there actually exist an object "infinity" that this sequence is converging to?
In other words, the question is: does there exist some topological space (that is, a set of objects plus a definition of what convergence means) which, as well as including the familiar real numbers we are used to, also includes an "infinity" concept to which some sequences of real numbers converge?
The answer is yes.
It is important to realize, though, that this topological space is not a number system. Although it includes an additional object called "infinity" as well as the familiar real numbers, you cannot add, subtract, multiply, or divide this additional object the way you can numbers.
Sometimes you will see a statement like "
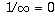 ". This does not really mean what it seems to say. You are not really dividing 1 by infinity. Instead, it is a statement about sequences. What it means is that if a sequence
". This does not really mean what it seems to say. You are not really dividing 1 by infinity. Instead, it is a statement about sequences. What it means is that if a sequence 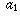 ,
, 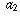 ,
, 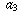 . . . converges to infinity, then the sequence of reciprocals
. . . converges to infinity, then the sequence of reciprocals 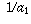 ,
, 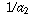 ,
, 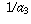 , . . . converges to zero.
, . . . converges to zero.(Similar looking expressions like "
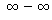 " don't make any sense, for just because two sequences
" don't make any sense, for just because two sequences 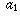 ,
, 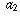 ,
, 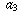 , . . . and
, . . . and 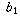 ,
, 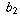 ,
, 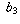 , . . . each converge to infinity tells you nothing about what the sequence
, . . . each converge to infinity tells you nothing about what the sequence 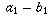 ,
, 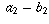 ,
, 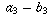 , . . . does.)
, . . . does.)More Information on Why "Infinity" Does Exist in the Context of A Topological Space

OK - so how many times do you half to cut the distance in half?
#192
Yeehaw
Originally Posted by Sly Raskal
Of course the plane would fly if the amount of thrust surpasses what the treadmill maximum speed is. I'm not debating that.
But did they match the treadmill speed to the amount of thrust the plane produced and if so did it then fly?
But did they match the treadmill speed to the amount of thrust the plane produced and if so did it then fly?
It wouldn't matter!
To use wstevens example, imagine holding a toy truck on a treadmill. The treadmill is spinning at 5mph. You can now easily push the truck forward, correct? If you turn the treadmill up to 10mph, you can still push the truck forward with the same amount of energy (+ a tiny amount to compensate for friction). At either speed, the 'thrust' to move the truck forward would be nearly identical to the thrust it would take on solid ground (again, only difference is friction).
Your arm moving the truck is the same as the jet engine on a plane. Its independent of the speed at which the treadmill is spinning.
#193
Nom Nom Nom Nom
Originally Posted by Sly Raskal
Of course the plane would fly if the amount of thrust surpasses what the treadmill maximum speed is. I'm not debating that.
But did they match the treadmill speed to the amount of thrust the plane produced and if so did it then fly?
But did they match the treadmill speed to the amount of thrust the plane produced and if so did it then fly?
#197
Go Giants
Two more Guinesses should do the trick....
#198
Originally Posted by BEETROOT
It wouldn't matter!
To use wstevens example, imagine holding a toy truck on a treadmill. The treadmill is spinning at 5mph. You can now easily push the truck forward, correct? If you turn the treadmill up to 10mph, you can still push the truck forward with the same amount of energy (+ a tiny amount to compensate for friction). At either speed, the 'thrust' to move the truck forward would be nearly identical to the thrust it would take on solid ground (again, only difference is friction).
Your arm moving the truck is the same as the jet engine on a plane. Its independent of the speed at which the treadmill is spinning.
To use wstevens example, imagine holding a toy truck on a treadmill. The treadmill is spinning at 5mph. You can now easily push the truck forward, correct? If you turn the treadmill up to 10mph, you can still push the truck forward with the same amount of energy (+ a tiny amount to compensate for friction). At either speed, the 'thrust' to move the truck forward would be nearly identical to the thrust it would take on solid ground (again, only difference is friction).
Your arm moving the truck is the same as the jet engine on a plane. Its independent of the speed at which the treadmill is spinning.
#199
Yeehaw
Originally Posted by Nineteen
Sorry, but that's a misleading analogy. The fact that you have to hold the toy truck means that you have to apply a certain amount of force to keep the toy from going backward. The thrust generated by the plane is the substitute for the act of holding the truck.
Theoretically you could simplify this question without changing the concept by stating there is zero friction.... the wheels would spin on the treadmill but the plane/truck would stay still above them.




